Истоки плохого мышления

О двух методах обучения. Откуда берутся взрослые люди с ограниченным мышлением, фанатики, безынициативные исполнители и просто-напросто тупицы? Естественно, вырастают из детей. Из тех, кому семья и школа не обеспечили более высокого уровня умственного развития. Конечно, ни родители, ни школа не могут сделать всех начинающими гениями. Но верно и то, что почти каждый выпускник мог бы быть гораздо более умственно развитым, чем это имеет место теперь. Что же этому препятствует? Таких тормозящих факторов немало. К ним относится, прежде всего, «нормальная наполняемость» классов, при которой ни один учитель не может создать каждому ученику оптимальный именно для него режим обучения.

Об это препятствие, как волны о скалу, разбивается много учительского труда и самоотверженности. Далее — несовершенство программ, учебников и методов обучения,недостаточно высокий уровень квалификации большого количества учителей. И наконец, то обстоятельство, что многим ученикам, именно таким, какими их формирует сегодняшнее обучение, трудно учиться из-за несоответствия их возможностей предъявляемым к ним требованиям.

Маленькие дети, осваивая родную речь и изучая окружающий мир, производят огромную умственную работу, нередко утомляя взрослых своими бесконечными «почему?». Но круг их знаний еще невелик, ум еще не сформировался, и их суждения полны милыми и нелепыми ошибками, которые так нравятся взрослым и которые фигурируют в печати под рубрикой «юмор в коротких штанишках». Их умственное развитие в основном осуществляется стихийно. Но вот ребенок приходит в школу, и школа начинает целенаправленно формировать его мышление. Каким оно будет «на выходе»? Кому будет вручен аттестат зрелости: творцу, «зубриле» или просто лодырю?

Создателю нового, пассивному исполнителю или просто бездельнику? В большой мере это зависит от методов обучения, которые в течение десяти лет будут направлять умственное развитие ученика.

Каковы же эти методы?

Один из них состоит в том, что учитель передает детям предусмотренную программой «сумму знаний», а учс ник должен воспринять рассказ, выучить дома по учебнику соответствующий материал и быть готовым к его пересказу. Учитель показывает, как решать задачу или выполнять упражнение, а школьник воспроизводит показанные ему способы действий.

Этот метод традиционен и, вероятно, существует столько же веков, сколько существует школа. Он называется объяснительно-иллюстративным1.

Суть другого метода в том, что школьник не получает знаний в готовом виде, а втянут в процесс активного поиска, своеобразного «открытия» новых для него явлений и закономерностей. В таком случае ученик становится в какой-то мере творцом и своего знания, и своего умственного развития. Этот метод называется проблемным2. Проблемный метод пока не имеет солидной истории, однако известно, что еще Сократ не излагал своим ученикам готовые знания, а приводил их к постижению этих знаний при помощи эвристической беседы, т. е. системы наводящих вопросов, отвечая на которые ученики постигали новые знания.

Проблемный метод, преимущество которого становится все более очевидным, еще не занял преобладающего места в школе, потому что он пока не «оброс» средствами реализации: в педагогической литературе по разным учебным предметам еще нет системы учебных заданий, которые позволили бы учителям регулярно проводить проблемные занятия. Объяснительно-иллюстративный метод, рассчитанный на умственную пассивность школьника, пока еще широко распространен. Это и накладывает отпечаток на умственное и нравственное развитие учащихся: получая в готовом виде плоды чужого умственного труда, они нередко привыкают жить чужим умом и уносят эту привычку в дальнейшую трудовую жизнь. Кроме того, при таком пассивном восприятии уже известного исчезает интерес, ибо ученик не чувствует себя открывателем.

Рис. А 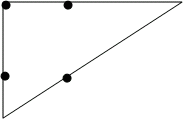Рис. Б

Ступить за тот заветный круг

Ступить за тот заветный круг. Оторвитесь от книги и попробуйте сложить четыре треугольника из шести спичек. Не возвращайтесь к чтению, пока не сделаете нескольких попыток.

Если вы не знали этой задачи раньше, вам пришлось изрядно поломать голову: вы не один раз перемещали так и сяк злополучные спички по поверхности стола и уже отчаялись найти решение. Но вдруг ваш взгляд случайно упал на забытый на столе пакет молока, и вы увидели, что перед вами не просто продукция молочной промышленности в удобной упаковке, а геометрическая фигура, имеющая четыре треугольника и шесть граней — треугольная пирамида, именуемая тетраэдром. И ваши спички сразу выстроились: три образовали треугольник, лежащий в основании, три другие поднялись над столом, образуя грани пирамиды, сходящиеся в одной точке — вершине.

Еще одна задача — «Четыре точки». Попробуйте провести через четыре точки (рис. 1а) три прямые линии, не отрывая карандаша от бумаги, так, чтобы карандаш вернулся в исходную точку. Автор этой задачи, психолог Я. А. Пономарев предложил ее 600 взрослым людям и все 600 безуспешно искали решение внутри квадрата, образованного четырьмя точками.

А оно было «так близко, так возможно»… Но ни один человек не догадался выйти за пределы квадрата и описать треугольник около него (рис. 1б)3.

А когда мы уже знаем решение, то кажется: что же может быть проще? И как это я сразу не додумался?

В чем же трудность решения задачи с шестью спичками и задачи «Четыре точки»? В том, что решение надо искать вне той области поиска, которая как бы сама собойнамечается условием задачи. В первой задаче говорится о треугольниках, и мы ищем плоскостное, а не объемное решение. Условия задачи не приковывают нас к плоскости, не запрещают выход в трехмерное пространство, но мы этого не понимаем. Мы видим только одно направление поиска, и переключиться на другое для нас невероятно трудно. То же и со второй задачей: ее условия совсем не предписывают искать решение внутри квадрата, но ведь квадрат нам дан готовенький, а другую область поиска еще надо найти. Какая же сила удерживает нас на плоскости или внутри квадрата, где мы бьемся в поисках решения, как мухи бьются о стекло? Извне — никакая. Мы сами. Зато способность преодолевать эти наши «внутренние барьеры» мышления и выходить в новые области поиска — одна из важнейших особенностей творческого мышления.

Люди, сумевшие выйти в новую область поиска, нередко находят легкие и красивые решения проблем, над которыми долго, мучительно и безрезультатно бьются те, кто не смог подняться над «внутренними барьерами». Интересный пример человека с таким складом ума — герой рассказов английского писателя Г. К. Честертона патер Браун, гениальный детектив в обличий скромного католического священника. Ему удавалось распутывать самые загадочные убийства, перед которыми становились в тупик слуги закона. Пока, например, они искали следы убийцы вокруг трупа и обшаривали окрестности, он поднимал глаза вверх и обнаруживал, что орудие убийства было сброшено с колокольни на проходящую внизу жертву или что тело было выброшено из окна верхнего этажа ближайшего дома. Но для этого надо было поднять глаза вверх, а никому, кроме патера Брауна, это не приходило в голову.

Чем большее число сторон, аспектов задачи видит и может охватить сразу, одним взглядом, решающий и чем различнее эти аспекты, тем лучше, — утверждает американский психолог Дункер. «Односторонность материала мысли», «бедность аспектами» является, по утверждению Дун-кера, основной характеристикой «плохого» мышления4.

Учим ли мы школьников искать новое направление поиска при решении задач, преодолевать «внутренние барьеры» мышления, находить новые повороты в решении вопросов? Это зависит от принятого нами метода обучения.

Если мы пользуемся объяснительно-иллюстративным и репродуктивным методами, то мы можем развить у школьников привычку к пассивному восприятию, бездумному заучиванию и шаблонным способам действий.

Если же мы пользуемся проблемным методом, при котором учащиеся систематически включаются в поиски путей решения проблемных вопросов и задач, можно ожидать, что результатом обучения будет развитие разностороннего, оригинального, не скованного узкими рамками мышления.

_____________

1Термин И. Я. Лернера.

2Эта же сущность обучения выражается в терминах «развивающееся обучение», «педагогика сотрудничества».

3См.: Пономарев Я. А. Психика и интуиция. — М., 1967.

4См.: Психология мышления/Под ред. А. М. Матюшкина. — М., 1965